特集詳細

自然科学における数学の重要な役割のひとつは自然現象および社会現象の数理的原理の解明です。私の専門分野である偏微分方程式論では、現象を数理的モデルである微分方程式として定式化し、その解析を通じて個々の現象を解明することを目的とします。このとき、数理解析の主たる特徴は、数多ある微分方程式をその構造にしたがって分類し、単純化・抽象化された指導原理によって、それらを統一的に理解する点にあります。

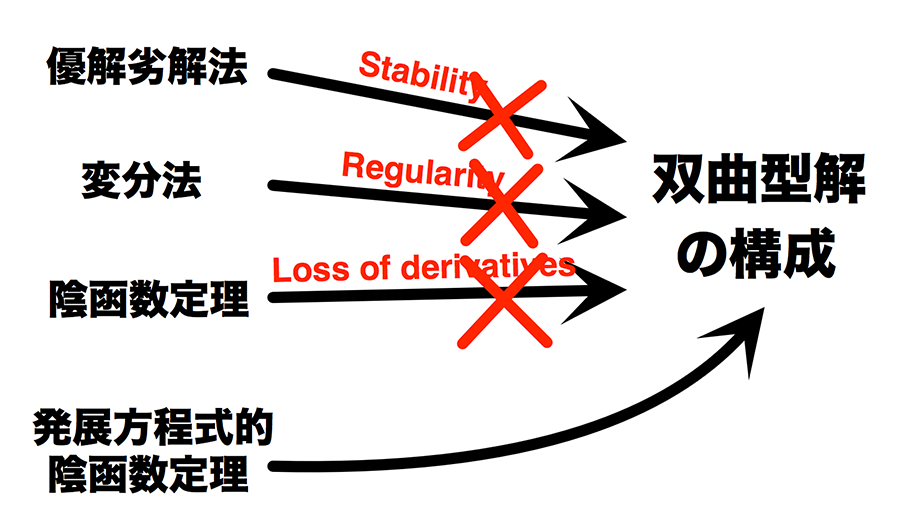
自由境界問題とは微分方程式の解の定義域自身も未知であるもので、氷の融解現象や最適投資問題などがその典型例となります。Bernoulliの自由境界問題は流体力学の逆問題や形状最適化問題として現れる古典的なものであり、優解劣解法や変分法、陰函数定理といった強力な解析手法によって研究が進められてきました。しかし、この問題は上記手法で構成可能な楕円型解とは異なる双曲型解とよばれる解を有することが分かっています。

Antoine Henrot氏（Elie Cartan研究所）との共同研究では、従来の非線型解析の適用が困難である双曲型解の構成を可能とする新しい解析手法を確立することに成功しました。この手法は抽象放物型方程式の最大正則性理論を基礎とする新しい型の陰函数定理で、仮想的に時間パラメータを導入して得られる発展方程式の可解性から元の問題の解の連続族を構成するというもので、正則性の損失（線型化作用素の逆作用素が正則性を十分に回復しないこと）をもつ非線型問題に一般に適用可能です。従来このような問題に対してはNash-Moserの陰函数定理が用いられてきましたが、その適用には技術的に難しい正確な非線型評価が要請されるとともに、得られる解は一般に初期値より正則性を失ってしまう欠点がありました。一方、本研究で導入された方法では、線型化作用素のスペクトル構造のみから解が構成されるともに、得られる解は同じ正則性のクラスに属すため、これを大域的解析、すなわち力学系的解析へと展開することが可能になります。また、線型作用素のスペクトル分布によって楕円型解と双曲型解の違いを明確に特徴付けた点は現象理解の観点から大変に意義のあるものです。今後の目標は、力学系的解析によって、重要未解決問題であるFlucher-Rumpf予想が主張する双曲型解の凝集現象を証明し、その数理的原理を解明することです。